Coupled Tensor Decomposition for Compact Network Representation

We highlight a key observation that drives our approach: within a convolutional layer, redundancy exists among the filters, as noted in various CNN compression studies, particularly in similarity-based filter pruning methods. Since all filters extract information from a common input, partially similar filters may produce partially similar output features. To enhance computational efficiency, the redundant computation of these similar parts should be avoided.

For example, in the top half of Figure 1, the filters \(\tens{W}_1\) and \(\tens{W}_3\) exhibit partial similarity, leading to their output feature maps \(\tens{O}_1\) and \(\tens{O}_3\) sharing a similar component (shown in blue) that is computed twice, causing redundant calculations. To avoid such duplicative computations and enhance efficiency, these filters can be jointly decomposed.

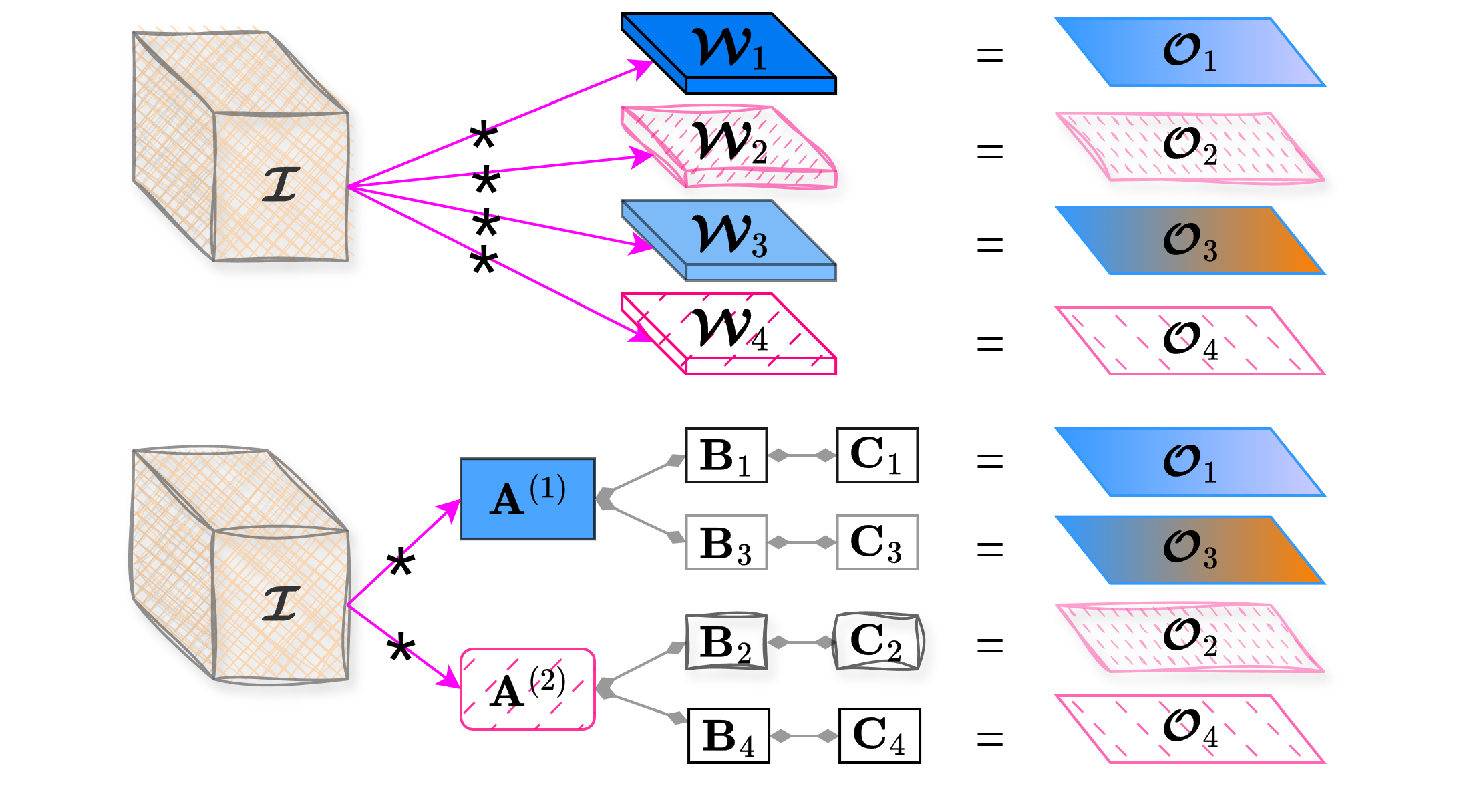
Building on these insights, we introduce the concept of coupled filters decomposition. In this scheme, multiple filters are jointly approximated using coupled tensor decompositions. To demonstrate the use of this method, we employ coupled CPD as a representative example due to its simplicity and efficiency, although our approach can be adapted to other decomposition techniques. Specifically, instead of decomposing each filter individually, we propose jointly factorizing them along a specific mode. After decomposition, the jointly decomposed filters share a common factor matrix in the selected mode while retaining their unique factor matrices in other modes.

This approach suggests that filters possess both common and particular characteristics. For instance, in the bottom of Figure 1, the two similar filters \(\tens{W}_1\) and \(\tens{W}_3\) are jointly factorized along the first mode, yielding a common factor matrix \(\matr{A}^{(1)}\) and different factor matrices in the other modes, namely matrices \(\matr{B}_1, \matr{C}_1\) and \(\matr{B}_3, \matr{C}_3\). Notably, since these filters share the same input tensor, the computation between the decomposed common factor and the input must only be performed once.

The central idea of CoDeC is to jointly factorize groups of similar filters along a specific mode, rather than decomposing each filter independently. To enable effective joint decomposition, the framework groups filters based on their similarity in the chosen mode, ensuring that filters within the same group exhibit higher similarity in the joint mode subspace compared to those in different groups. To achieve this, CoDeC adopts a two-stage process, as illustrated in Figure 2, consisting of the following components:

1. Clustering: The filters of the original convolution layer are classified into \(K\) clusters, as illustrated in the left half of Figure 2.
2. Coupled decomposition: Filters within each cluster are jointly decomposed using coupled CPD. The decomposition processes across all \(K\) clusters are depicted in the right half of Figure 2. Once all clusters are processed in parallel, the output factor matrices are combined to form the CoDeCBlock (Figure 3).

This scheme is simultaneously applied to all convolution layers of the original model.

To demonstrate the adaptability of CoDeC, we assess 4 architectures: VGG-16, ResNet-20/32/56/110 with residual blocks, DenseNet-40 with dense blocks, and SqueezeNet with fire modules. These models are tested on the CIFAR-10/100 dataset. Additionally, to validate the scalability of CoDeC, experiments are conducted on the ImageNet dataset using ResNet-18/32/50/152 architectures. Furthermore, the compressed ResNet-50 model is employed as the backbone network for FasterRCNN, MaskRCNN, and KeypointRCNN on the COCO-2017 dataset. We compare CoDeC with more than 50 related works, as detailed in the paper, and present ResNet-50 results on ImageNet in Table 1 for clarity. Our method consistently surpasses other approaches across all compression levels in terms of performance and complexity reduction.